Fördelningar för observationer och skattningar
Insamlade data från en inventering används i första hand för att skatta populationsvärdet Y och dra slutsatser rörande måluppfyllelsen. För fördjupade studier t.ex. för jämförelser mellan delpopulationer eller olika tidpunkter, för analys av trender och trendbrott används olika statistiska metoder. Dessa metoder förutsätter regelmässigt vissa egenskaper hos data. Till dessa hör villkor som ”(stokastiskt) oberoende” och ”normalfördelning”. Vi ska helt kort diskutera dessa nedan.Oberoende
Begreppet stokastiskt oberoende har en strikt matematisk definition, vilken inte är så lätt att skapa sig en intuitiv bild av. Men om man tänker sig att man gör två observationer, y1 och y2 av en population, där vi observerar y1 först. Om dess värde inte ger någon information om värdet av y2 så är observationerna oberoende. Det är klart att om vi inte vet medelvärdet i populationen så ger y1 information om y2 så vi betraktar här populationsmedelvärdet som ”känt”. Oberoende observationer innebär att varje ny observation bär med sig helt ny information. Vid sampling OSU (eller PPS) ”med återläggning” får man garanterat oberoende observationer. Det är enklare att beskriva situationer där oberoende inte gäller än att ge en verbal definition av begreppet och vi tar nedan upp de vanligaste fallen där beroende kan förutsättas.Det ska först påpekas att eventuellt beroende bland observationerna påverkar analyser endast om man baserar dessa på enskilda observationer. För skattningar påverkas beräkningen av medelfel. Dock kan även skattningar vara stokastiskt beroende.
Den statistiska effekten av beroende är att det ”faktiska” antalet observationer inte är detsamma som det ”formella”. Ett extremt (tankemässigt) fall av beroende är att betrakta samma objekt säg tre gånger. Vi har då formellt tre gånger så många observationer som det faktiska antalet.
Urval utan återläggning
För urval utan återläggning (i en ändlig population) är successiva observationer inte oberoende eftersom vi genomgående samplar nya objekt (redan observerade objekt med sina värden är uteslutna). Detta beroende är dock normalt negligerbart eftersom samplen normalt är mycket små i förhållande till populationsstorleken.Hierarkiskt insamlade data
Vid två- eller flerstegsurval är de enskilda observationerna inte oberoende. Om vi först lottar bestånd och sedan objekt inom provytor i bestånd så är observationerna från ett och samma bestånd inte oberoende. De tenderar alla att antingen ligga över eller under populationsmedelvärdet och detta beroende på gemensamma beståndsegenskaper. För analys av data ska orsaken till beroendet ingå i den statistiska modellen (t.ex. med en stokastisk komponent ”bestånd”).Klusterurval
Vid klusterurval måste man anta att observationerna inom ett kluster uppvisar beroende, på samma sätt som för hierarkiskt insamlade data i allmänhet (och beroendet kan också modelleras på samma sätt).Data med rumslig korrelation
Med rumslig korrelation menas (ungefär) att värden från närliggande objekt är mer lika varandra än värden från objekt ”i allmänhet”. Förhållandet kan studeras med metoder inom området spatial statistik (spatial autokorrelation). Det här kan t.ex. inträffa om man lägger ut (relativt närliggande) provytor i kluster som i Riksskogstaxeringen. Där ”undviker” man problemet genom att använda klustervärden som analysenheter. (Klustren ligger på långa avstånd från varandra).Upprepade mätningar (temporal autokorrelation)
Vid återinventering av samma objekt är observationerna från samma objekt inte oberoende. Värdena för enskilda objekt varierar inte slumpmässigt utan är korrelerade i tiden. Det finns flera angreppssätt vad gäller statistisk modell.Helhetsperspektiv
För att komplicera det hela är frågan om oberoende eller ej inte ”absolut” utan måste betraktas från ett ”helhetsperspektiv”. Om vi samplar (via provytor) OSU (med återläggning) i ett bestånd är observationerna oberoende så länge vi bara betraktar beståndet. Men om vi samplar i flera bestånd och betraktar helheten (alla data, hela populationen) blir inte observationerna från ett och samma bestånd längre oberoende. Den ”omgivande” populationen spelar alltså roll (på samma sätt som den gör för medelvärde, standardavvikelse etc.).Skattningar kan vara beroende
Även skattningar kan uppvisa beroende. Framför allt kan skattningar som görs vid upprepade tillfällen vara beroende (jfr upprepade mätningar ovan). Detta har betydelse för studier av förändringar och trender.Beroende mellan variabler
Skattningar av olika storheter, t.ex. stamantal och volym för bestånd är också beroende, men av helt andra skäl än av designen. Här uppstår beroendet på grund av att variablerna i sig uppvisar samband och inte på grund av hur urvalet görs.Normalfördelning
För många analysmetoder är normalfördelning ett (formellt) villkor. För att pröva om data är normalfördelade finns ett antal tester som finns i vilket statistikprogram som helst. Det är dock långt ifrån alltid nödvändigt att (enskilda) data följer en normalfördelning för att de statistiska metoderna ska fungera. Vi tar upp några fall.Skattningar och deras medelfel
Skattningar av populationsvärden kräver inte normalfördelning (för de enskilda värdena). Det gör inte heller beräkning av deras medelfel. (Det finns i detta sammanhang inte heller några sådana formella villkor).Data att användas i linjära modeller
Det är inte ovanligt att forskare tror att rådata till variansanalys eller regressionsanalys måste vara normalfördelade. Så är inte fallet. Det är avvikelserna mellan observerade värden och modellparametrarnas värden, residualerna, som (helst) ska vara normalfördelade.Normalfördelade avvikelser (residualer) i linjära modeller
För att skattningar av parametrar i t.ex. en regressionsanalys ska vara väntevärdesriktiga räcker det om avvikelserna har väntevärdet 0, alltså att data inte avviker systematiskt från populationen i övrigt. Däremot kan testers ”p-värden” påverkas. Simuleringar visar dock att denna påverkan är mycket ringa (vad gäller så kallade fixa effekter, alltså konstanter som ingår i modellen). Att data inte är normalfördelade är alltså inte bra, men det är normalt inte allvarligt. Orsaken är att skattningar av parametrar är vägda medelvärden och sådana är oftast approximativt normalfördelade för någorlunda stora sampel. Detta beror på en sats som går under namnet Centrala gränsvärdessatsen (flera varianter av den finns).Test av måluppfyllelse
För exemplen på hypotesprövning av måluppfyllelse har antagits att skattningen är normalfördelad. Så är approximativt fallet även om de enskilda värdena inte är det och orsaken är åter Centrala gränsvärdessatsen. Vi visar ett exempel, där en population (med 500 objekt) har simulerats och där enskilda värden långtifrån uppvisar normalfördelning (den är i själva verket ”lognormal”). Ur populationen har 1000 sampel om storleken n=30 samplats, dels OSU och dels PPS mot en korrelerad variabel (x). I fallet OSU har också kvotskattningen (med x) testats. Resultatet (skattat medelvärde) visas nedan med några histogram (med anpassade normalfördelningar). Histogrammen visarFigur 1: Populationsvärden,
Figur 2: Relationen mellan hjälpvariabeln x och målvariabeln y,
Figur 3: Fördelningen för skattade värden med OSU-urvalet (utan användning av x),
Figur 4: Fördelningen för kvotskattningarna och
Figur 5: Fördelningen för skattade värden med PPS-urvalet.
Som synes följer de tre fördelningarna för de skattade värdena mycket väl de anpassade normalfördelningarna trots att populationsvärdena inte gör det (i och för sig upptäcker vissa tester i vissa fall avvikelser från normalfördelningen för skattningarna, men de avvikelserna torde vara rätt betydelselösa).
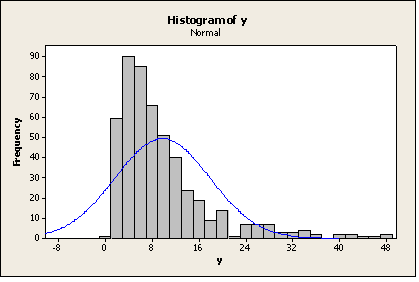
Figur 1: Populationsvärden
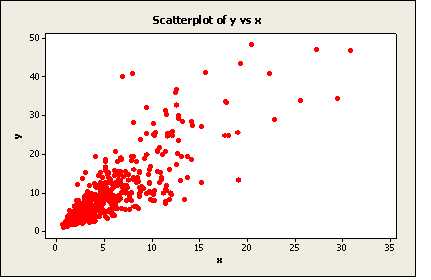
Figur 2: Samband mellan x och y
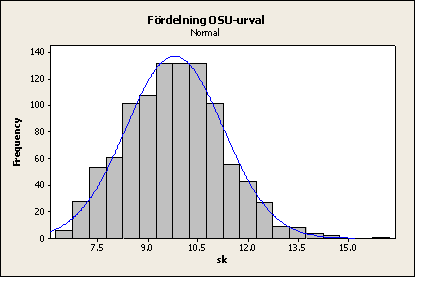
Figur 3: OSU-urval
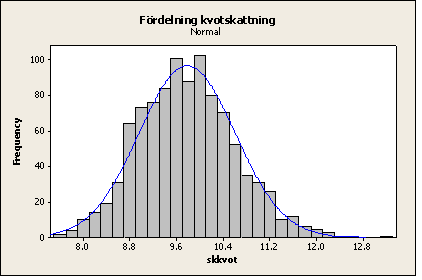
Figur 4: Kvotskattning
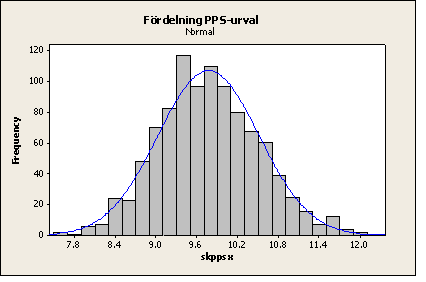
Figur 5: PPS-urval
De empiriska standardavvikelserna för skattningarna med PPS-urvalet och kvotskattningen är cirka 50-55 % (PPS minst) av det rena OSU-fallet. Detta motsvarar ungefär samma precision med 25-30 % av sampelstorleken i OSU-fallet. Alltså med n=30 i fallet PPS skulle vi behöva cirka n=120 i fallet OSU för att uppnå samma precision här.


