Principalkomponentanalys
Principalkomponentanalys (PCA, Principal Components Analysis) är en standardmetod för att beskriva och visualisera likheter och olikheter mellan prover i ett multivariat dataset där data har linjär respons, vilket är fallet när man inte har förekomst av organismer som responsdata. Har man organismer som responsdata används korrespondensanalys (Correspondence Analysis, CA) och besläktade metoder på motsvarande sätt (se flödesschemat). PCA (liksom CA för andra typer av data) används ofta för att studera, lära känna och hitta mönster hos sina data. Exempel på mönster kan vara korrelationer, grupperingar och avvikande värden. Både PCA och CA har kallats för hypotesgenererande metoder för att de snabbt sammanfattar ett stort dataset till några få observerbara gradienter (de olika axlarna i ett ordinationsdiagram).I introduktionen till multivariata metoder visades hur likhet och olikhet mellan olika figurer kunde illustreras med hjälp av PCA:
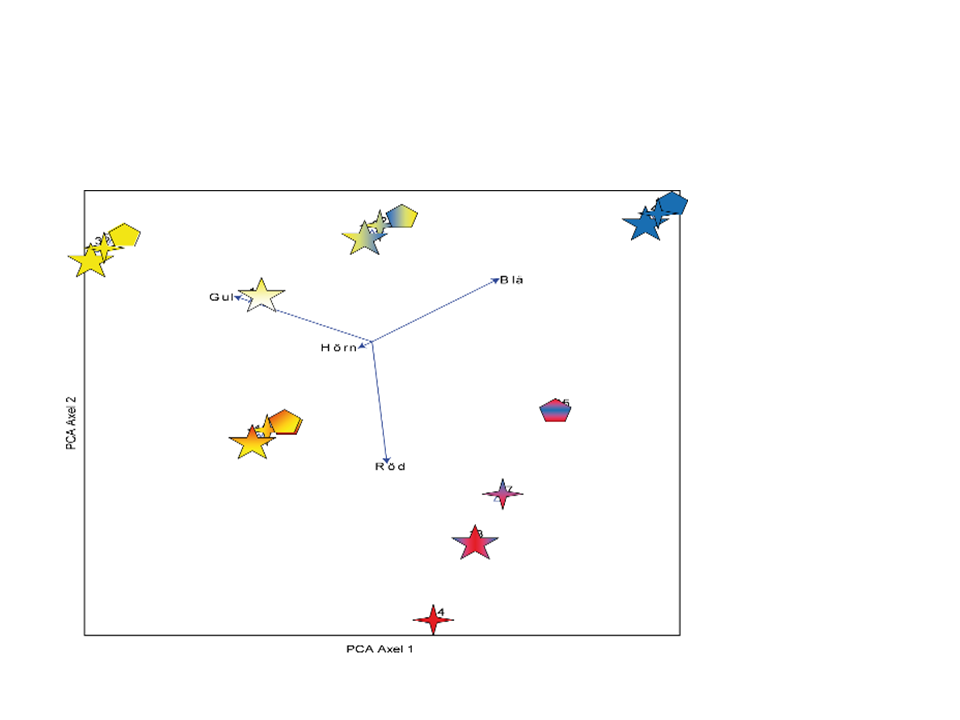
PCA extraherar den starkaste gradienten i ett dataset och uttrycker den längs den första ordinationsaxeln. Den näst starkaste gradienten i data uttrycks längs axel 2. I exemplet i figuren ovan illustrerar axel 1 en gradient från gul till röd/blå. Axel 2 skiljer ut de röda figurerna från de gula och blåa.
Man kan välja vilken information som ska illustreras i ett ordinationsdiagram. I PCA-exemplet ovan visas både objekten och beskrivningsvariablerna, men beroende på frågeställning och antal prover kan man välja att bara ha med objekt eller bara beskrivningsvariabler.
Förklarad variation
I vissa dataset finns det starka gradienter, medan andra data inte har det. Oavsett vilket kommer en ordination att extrahera gradienter. Om det finns starka gradienter kommer den del av den totala variationen som förklaras av en axel att vara hög.Den förklarade variationen uttrycks i egenvärden. Varje axel har ett egenvärde. Den andel av variationen som en axel förklarar får man genom att dividera axelns egenvärde med den totala variationen (detta görs automatiskt i många program). I en PCA är den totala variationen lika med antalet beskrivningsvariabler (4 i exemplet ovan). I exemplet ovan med ett avvikande värde förklarade axel 1 betydligt mer av den totala variationen än när det avvikande värdet var korrigerat (Tabell 1)
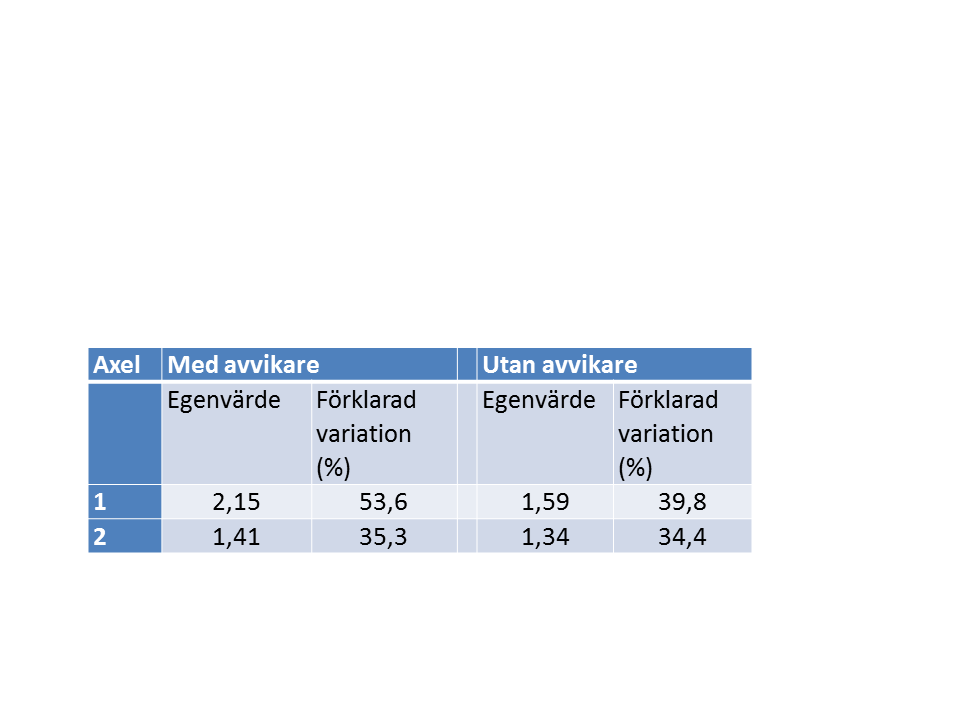
Tabell 1. Egenvärden och variation för exemplen i figur 1. Med ett avvikande värde uppstår en stark gradient mellan det avvikande provet och övriga prover, och som uttrycks längs den första ordinationsaxeln som förklarar mer än hälften av den totala variationen i datasetet. Den totala variationen är i båda fallen 4 (= antalet beskrivningsvariabler).
Olika varianter av PCA
Det finns lite olika varianter av PCA. Vilken variant som används beror på vilken typ av data man har (Tabell 2). Olika program har olika förvalda typer av PCA. Det är viktigt att ta reda vilken variant av PCA som är förvald, och hur man ändrar till rätt variant.
Exempel på olika tillämpningar med PCA
- Exemplet i figuren ovan, finns närmare beskrivet i PCA Exempel 1.
- Ett annat exempel är en PCA på det klassiska datasetet med längd på kron- och stödblad hos olika arter av växten iris, PCA Exempel 2.
- Ett tredje exempel beskriver hur man kan använda PCA för att studera förändringar över tid, PCA Exempel 3 (Hälsohem).
Olika typer av data
Data som är avstånd mellan prover
När man har data som uttrycker skillnader mellan olika observationer har man data i en symmetrisk tabell. Skillnaderna kan antingen vara geografiska som i en avståndstabell för olika städer, eller beräknade med någon formel för t.ex. florisitiskt eller genetiskt avstånd. I dessa fall kan PCA användas för en översikt. För PCA på denna typ av data använder man den variant av PCA som utförberäkningen på centrerade data. Även om PCA fungerar för data som beskriver avstånd är PCoA (Principal Coordinates Analysis) en bättre metod för att analysera rena avståndstabeller (PCoA kallas även MDS Multi Dimensional Scaling).Data med differenser, före-efter
När man har data av typen före/efter vill man veta vad som hänt med varje observation som följd av t.ex. en behandling. Denna typ av data kan analyseras med PCA i två steg.- Först gör man en PCA där alla observationerna finns med två gånger, en rad för Före och en rad för Efter. I det resulterande ordinationsdiagrammet kan man se hur varje observation flyttat sig från Före till Efter. Vissa program kan sammanbinda punkterna för Före och Efter med en pil.
- Nästa steg är att göra ett differensdataset, med differenser Efter-Före. Man kan också ta med bakgrundsvariabler som är konstanta mellan Före och Efter. En PCA på differensdatasetet kan visa vari skillnaderna ligger. I denna analys är det viktigt att inte låta programmet centrera data (dvs. subtrahera med medelvärdet) innan beräkningarna för PCA:n. En centrering skulle eliminera huvudeffekten och bara behålla bara variationen, och då tappar man effekten av ”behandlingen”. I exemplet PCA Exempel 3 (Hälsohem) finns ett exempel på analys av differenser.
Viktigt att veta
Skalning
I en del program skalas alla variabler automatiskt innan beräkningarna i en PCA sker. Det kan vara centrering eller både centrering och standardisering. I avsnittet Olika varianter av PCA ovan listas skillnaderna mellan olika varianter av PCA, och vilken skalning som ska användas. De flesta program för PCA har möjligheter att ändra skalningsförfarandet. Om man använder fel skalning blir resultatet felaktigt!Fallgropar
Om man har data som har så kallad unimodal respons (dvs. förekomsten av djur eller växter), så ska Correspondence Analysis, CA och besläktade metoder användas. En PCA på data med unimodal respons ger direkt felaktiga resultat!Detaljer
Generell beskrivning
Allt som beskrivs i detta stycke sker automatiskt i beräkningarna för PCA. Denna beskrivning är bara för en orientering av hur beräkningarna går till.Som ordet pricipalkomponent antyder så finner PCA dominanta komponenter i data. Den mest dominanta komponenten är komponent eller axel 1, PC1, och illustreras per definition som den horisontella axeln i ett ordinationsdiagram. Låt oss föreställa oss ett koordinatsystem med lika många axlar som variabler i data (hyfsat enkelt i teorin men inte i praktiken!). I detta koordinatsystem kan vi lägga in varje observation från våra data. Då alla observationer finns där har vi en multidimensionell punktsvärm av data. PC1 utgörs av den riktning i denna multivariata rymd längs vilken punktsvärmen har sin största spridning. Nästa komponent, PC2, är den riktning, vinkelrät mot den första, som data har sin största spridning (alltså näst största totalt sett). Den tredje komponenten kommer att ligga vinkelrät mot de båda tidigare och finna den tredje mest dominanta riktningen, osv. Observationernas läge längs de extraherade komponenterna kallas på engelska för scores. På svenska använder man ibland uttrycket position längs en axel.
Beskrivningsvariablernas position längs komponenterna (ordinationsaxlarna) beräknas genom linjär regression med provernas position längs en ordinationsaxel som x-variabel och det uppmäta värdet för en beskrivningsvariabel i respektive prov som y-variabel. Positionen för beskrivningsvariabeln längs den axeln blir då riktningskoefficienten för en regressionslinje för detta samband (se figuren nedan). Om en beskrivningsvariabel uppvisar en stark gradient längs den testade axeln kommer lutningen på regressionslinjen att var stor. Om beskrivningsvariabeln är okorrelerad till axeln i fråga kommer lutningen (och därmed positionen längs axeln) att närma sig 0.
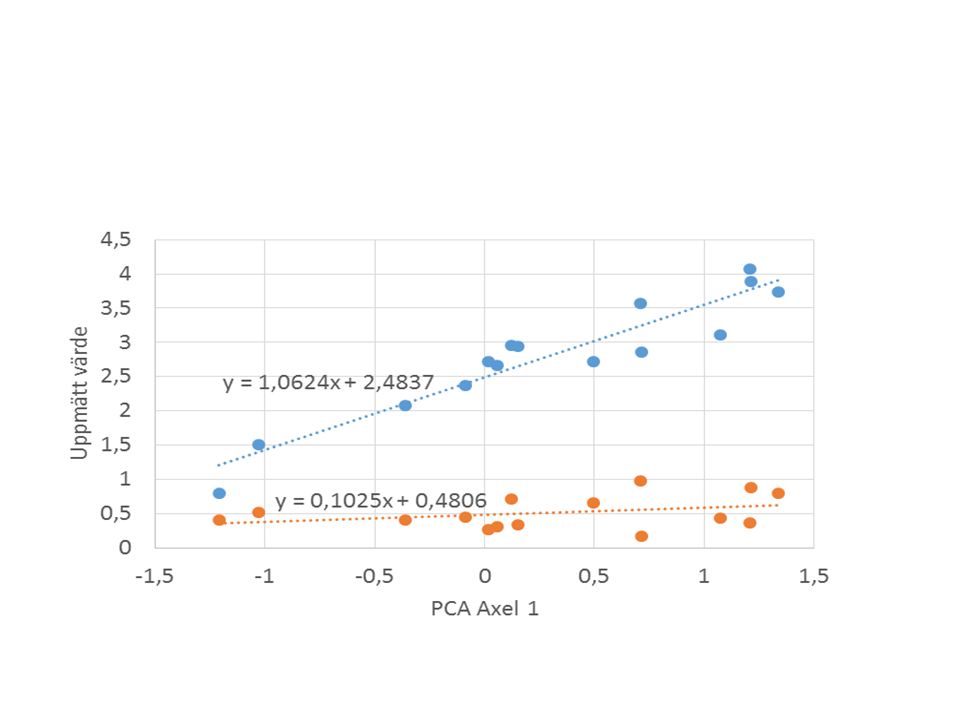
Samband mellan provers positioner längs PCA-axel 1, och värdet på två beskrivningsvariabler. Beskrivningsvariablernas position längs ordinationsaxeln ges av lutningen på regressionslinjen i sambandet i figuren. I detta fall 1,06 för den blåa variabeln och 0,10 för den röda.
Antal ordinationsaxlar
Antalet ordinationsaxlar (eller komponenter) som man beräknar beror på syftet. I de flesta fall räcker det med 2 axlar. Egenvärdena för de olika axlarna ger en god vägledning om hur många axlar som är lämpligt att visa. Vissa program ger en så kallad ”scree plot” som visar hur mycket av variationen de olika ordinationsaxlarna representerar. Om axel 2 och 3 har ungefär samma egenvärden bör man antingen göra en tredimensionell plot, eller plotta axel 1 mot axel 3 för att se om detta visar viktiga gradienter och samband i data.Teoretiskt kan man beräkna lika många axlar för ett dataset som det finns beskrivningsvariabler eller objekt (prover), beroende på vilket av dessa två som är lägst. Med så många axlar har man dock inte åstadkommit något annat är en rotation av det ursprungliga multidimensionella koordinatsystemet. En tanke med alla indirekta ordinationer är att man vill skilja ut det som är struktur i data från det alltid närvarande bruset. Då vill man ha en stoppregel som säger att hit men inte längre finns det struktur i data, resten är brus. I PCA är den enklaste stoppregeln är att axelns egenvärde skall vara större än 1.0 (andra värden gäller för andra ordinationsmetoder!). En mer sofistikerad stoppmetod som är inbyggd i programmet Simca är att för varje ytterligare komponent utesluta element i data, räkna delmodell med dessa uteslutningar och sedan använda modellen för att prediktera de uteslutna elementen. Om prediktionsfelet inte är för stort accepteras komponenten, annars stoppar man. Denna metod kallas korsvalidering.
Variabeltyper
PCA kan hantera både kvantitativa och kvalitativa variabler. Kvalitativa variabler måste dock expanderas till lika många 0/1-variabler (s.k. Dummy-variabler) som det finns nivåer i den kvalitativa variabeln (Tabell 3). I många program görs dummy-transformeringen automatiskt, och är i så fall inget man behöver fundera över.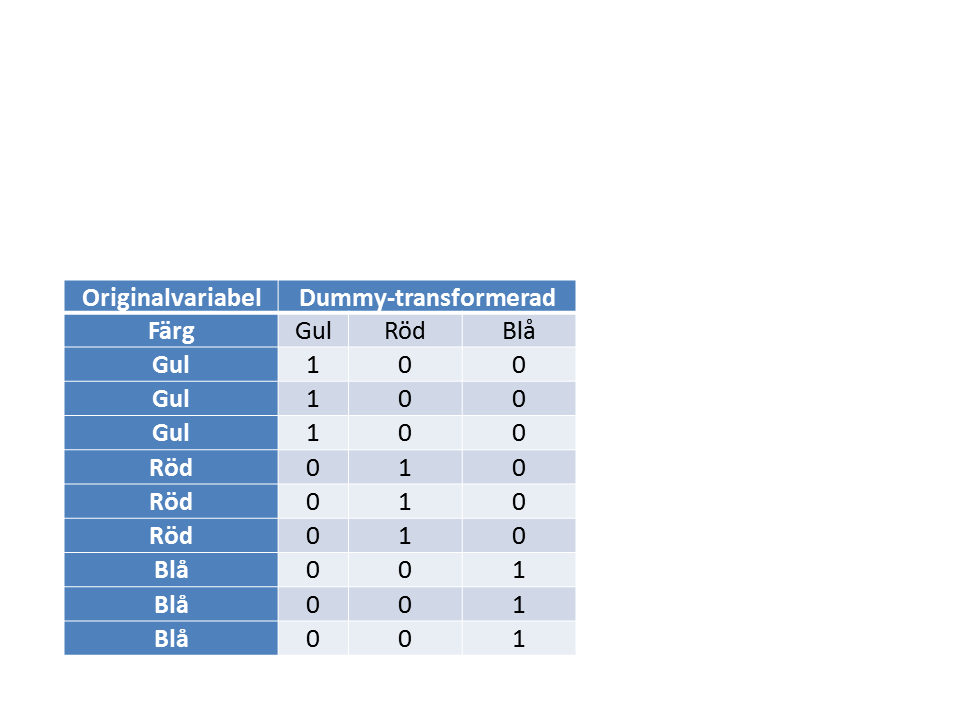
Tabell 3. Exempel på dummy-transformering av en kvalitativ variabel (Färg) till tre kvantitativa variabler som kan användas i en numerisk analys.
Hantering av värden under detektionsgräns och saknade värden
Några program har förvalda rutiner för att hantera saknade värden. Det är viktigt att undersöka hur saknade värden hanteras i det program man använder. En del program tar bort hela den rad där det saknas ett värde, medan andra program tar bort hela kolumnen. Några program använder någon form av modellering för att skatta saknade värden.Man måste som användare fundera över hur man ska låta sitt program hantera sakande data, och inte tro att programmet löser problemet genom trolleri. Om programmet t.ex. har som förvald metod att ta bort hela den rad där det finns ett saknat värde måste man vara medveten om detta och fundera om det kanske är bättre att manuellt ta bort kolumnen istället, innan man börjar räkna.
För data under detektionsgränsen måste något numeriskt värde anges. Se vidare om detta i avsnittet om Värden under detektionsgräns.


