Olika variabeltyper (datatyper) – olika metoder
För att kunna avgöra vilken metod som ska användas för att analysera ett befintligt dataset måste man först bestämma vilken typ av data man har samlat in. Ofta faller observationerna i en av följande kategorier:- Kontinuerliga värden, som kan anta alla värden inom ett variationsområde, t.ex. koncentrationsmätningar
- Räknedata, antalsdata, som bara kan anta heltal och uppstår när man räknar en slumpmässig händelse, t.ex. antal fjärilar på en plats
- 0/1 eller binära data, som bara kan anta två olika värden, t.ex finns/finns inte eller över/under ett gränsvärde
- Kategorisk data, som kan anta ett fåtal olika värden, som t.ex. hög/medium/låg eller röd/grön/blå
Kontinuerliga variabler
Genomsnittsvärden - normalfördelade variabler
I många fall är man intresserat i att undersöka hur genomsnittsnivån värden av en kontinuerlig variabel kan beskrivas (t.ex. om det finns en trend, samband till andra variabler). Modeller som är användbara i detta fall är de som oftast lärs ut först i grundläggande statistikkurser (länk kompendium) och baseras ofta på antagande att variabeln är normalfördelat. Detta antagande måste kontrolleras i samband med analysen.I de flesta analyserna gör man en kontroll av antaganden efter man har anpassat en modell eller utfört en analys. Även om variabeln man undersöker inteär normalfördelat, så är det ibland möjligt att använda standardmetoder i alla fall, t.ex. om man jobbar med medelvärden på tillräckligt många observationer (jmf centrala gränsvärdesatsen) eller om man har möjlighet att erhålla en normalfördelning genom transformation. Observationer av koncentrationer visar, till exempel, ofta en log-normalfördelad form. Genom log-transformation kan man då göra observationerna normalfördelade och standardstatistikmetoder kan användas om de passar frågeställningen.
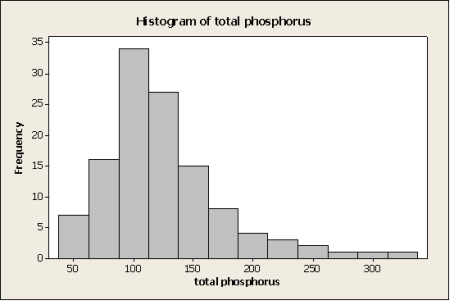
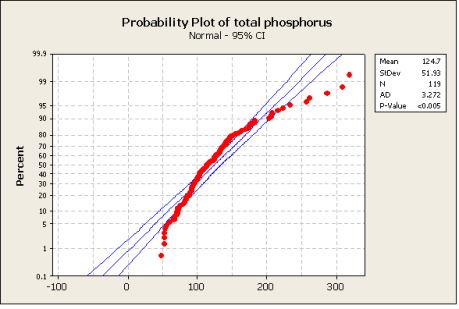
Figur 1:Totalfosfor i Skivarpsån under åren 2000-2010. Bild 1: koncentrationsmätningarna visar en log-normal form. Bild 2: Efter transformation skulle metoder som baseras på normalfördelning kunna användas.
Många statistiska metoder baseras på ytterligare antaganden, t.ex. att varianserna ska vara lika i de olika grupperna man undersöker (t-test, variansanalys) eller över det undersökta området (regression). Ett mycket viktigt antagande som många statistiska metoder vilar på är att observationerna i analysen ska vara oberoende.
Extrema händelser
Det är inte alltid mest intressant att undersöka genomsnittsvärden. Vill man undersöka förändringar över tiden kan det vara så att genomsnittsnivåer inte ändras alls eller bara lite, medan extrema händelser (stormar, översvämningar, torka, överskridande av gränsvärden,…) blir mer extrema eller inträffar allt oftare. För att beskriva extrema händelser kan man titta på observerade percentiler (förklaring: värdet, där enbart en viss procentsats av alla observationer ligger ovanför. T.ex. 95% percentilen: bara 5% av alla observationer är större än detta värdet). Man kan också använda statistiska fördelningar för att beskriva extremvärden, t.ex. generalised extreme value distribution (GEV) eller peak-over-threshold distribution (POT).Genomsnittsvärden - Ingen känd fördelning
I vissa fall går det inte att hitta någon passande statistisk fördelning för det observerade datamaterialet. En del frågeställningar kan då analyseras med icke-parametriska metoder, som baseras på rangordning av data, på medianer eller percentiler istället för en känd statistisk fördelning. Observera dock att även dessa metoder kan baseras på vissa antaganden som måste vara uppfyllda för att analysen ska vara korrekt.Räknedata – antalsdata
En annan typisk uppsättning av observationer i miljöanalys är räknedata eller antalsdata. Dessa uppstår när man räknar t.ex. antal individer på en viss plats. Vill man analysera dessa data genom att undersöka samband till andra variabler utgår man oftast ifrån att antalsdata är Poisson-fördelat och använder Poissionregression. När man använder Poissonfördelningen så utgår man ifrån att individerna uppträder oberoende från varandra. Detta antagande är inte uppfyllt när man observera en art som uppträder i grupp. Då kan man dock i vissa fall använda negativ binomial fördelning istället. Ett annat typiskt problem med antalsdata uppstår när man observerar sällsynta arter och resultaten ofta blir noll. Även för dessa fall finns det statistiska fördelningar som tar hänsyn till denna egenskap, de kallas ofta för ZIP – zero inflated poissonfördelning.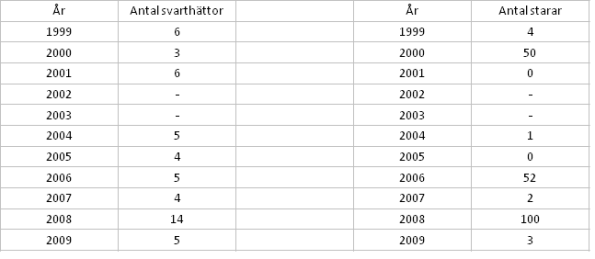
Tabell 1: Antal svarthättor och antal starar i samma område under 11 år. År 2002 och 2003 oberverades inte detta område.
I tabell 1 kan man se antal svarthättor under 11 år. Poissonfördelning skulle kunna användas för att modellera observerat antal svarthättor. Starar däremot uppträder i flock och antaganden om oberoende mellan observationerna är inte uppfylld.
Kategoriserade och Binära (0/1) variabler
Binära data, alltså data som bara kan anta två olika värden, kan påträffas i miljöanalysen när man undersöker förekomsten av arter (finns/finns inte) eller överskridande av gränsvärden (över/under). När en variabel bara kan anta två olika värden, så kan sannolikheterna för denna variabel ofta beskrivas med binomialfördelningen. Har man fler än två klasser, t.ex. olika ekologiska statusklasser, så används multinomialfördelning i en modellering av dessa. IVill man modellera förekomsten eller överskridande med hjälp av förklarande variabler, så använder man oftast logistisk regression eller, mer allmänt, generaliserade linjära modeller (extern länk, engelska) eller generaliserade additiva modeller (extern länk, engelska). Liknande modeller använder man när man har fler än bara två kategorier.


